[ML] : 02. 회귀 분석

서론

• 이번 포스팅에서는 회귀(Regression)에 대해서 알아보도록 하겠다.

01. 회귀

1) 회귀(Regression)란?

• 회귀는 종속 변수(y)와 독립변수(x)간의 관계성을 찾는 것으로, 독립변수 값을 통해서 종속 변수를 예측하는 것이다. 예를 들면 학생의 학습량에 따라서 성적을 분석한다고 했을때, 여기서 성적이 종속변수, 학습량이 독립변수가 된다. 학습량이 늘면 성적이 올라간다면 독립변수의 값이 올라가면 종속변수의 값 또한 값이 올라가는 선형적인 관계를 가진다고 얘기할 수 있다.
  

• 이렇게 관계성을 예측(새로운 데이터에 대한 종속 변수의 값 변화 예측)하거나 추론(독립 변수들이 종속 변수에 미치는 영향을 추론)하는 것이 회귀모델이다.
  

• 독립변수
  • 결과(종속 변수)에 영향을 미치는 요인
  • 모델 학습에서는 학습 데이터의 입력
    
• 종속변수
  • 요인(독립 변수)에 의해 나타나는 결과
  • 모델 학습에서는 학습 데이터의 정답(Label, Target)
    

[참고: https://wendys.tistory.com/169]

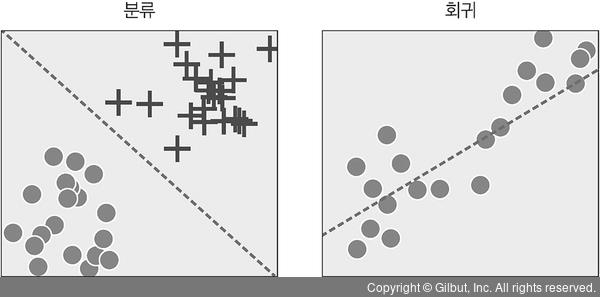
2) 분석 유형에 따른 분류

• 선형 회귀
  • 선형 회귀는 독립 변수와 종속 변수 사이 관계가 선형적으로 표현하는 회귀 유형이다. 해당 문제를 대표하는 직선을 찾는것이다. 이를 수식으로 나타내면 아래와 같다.
  \[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n + \epsilon\]
  • $( y )$는 종속 변수
  • $( x_1, x_2, \ldots, x_n )$는 독립 변수
  • $( \beta_0 )$는 절편 (intercept)
  • $( \beta_1, \beta_2, \ldots, \beta_n )$는 기울기
  • $( \epsilon )$은 오차 항 (error term)

• 다항 회귀
  • 독립 변수와 종속 변수 사이 관계를 비선형적으로 표현하는 회귀 유형이다. 이를 수기으로 나타내면 아래와 같다.
  \[y = \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_3 x^3 + \cdots + \beta_k x^k + \epsilon\]
  • $( y )$는 종속 변수.
  • $( x )$는 독립 변수.
  • $( \beta_0, \beta_1, \beta_2, \ldots, \beta_k )$는 회귀 계수.
  • $( k )$는 다항식의 차수(degree).
  • $( \epsilon )$은 오차 항.

3) 독립/종속 변수 개수에 따른 분류

• 독립 변수
  • 1개 : 단순 회귀
  • 2개 이상 : 다중 회귀
    
• 종속 변수
  • 1개 : 단변량 회귀
  • 2개 이상 : 다변량 회귀
    

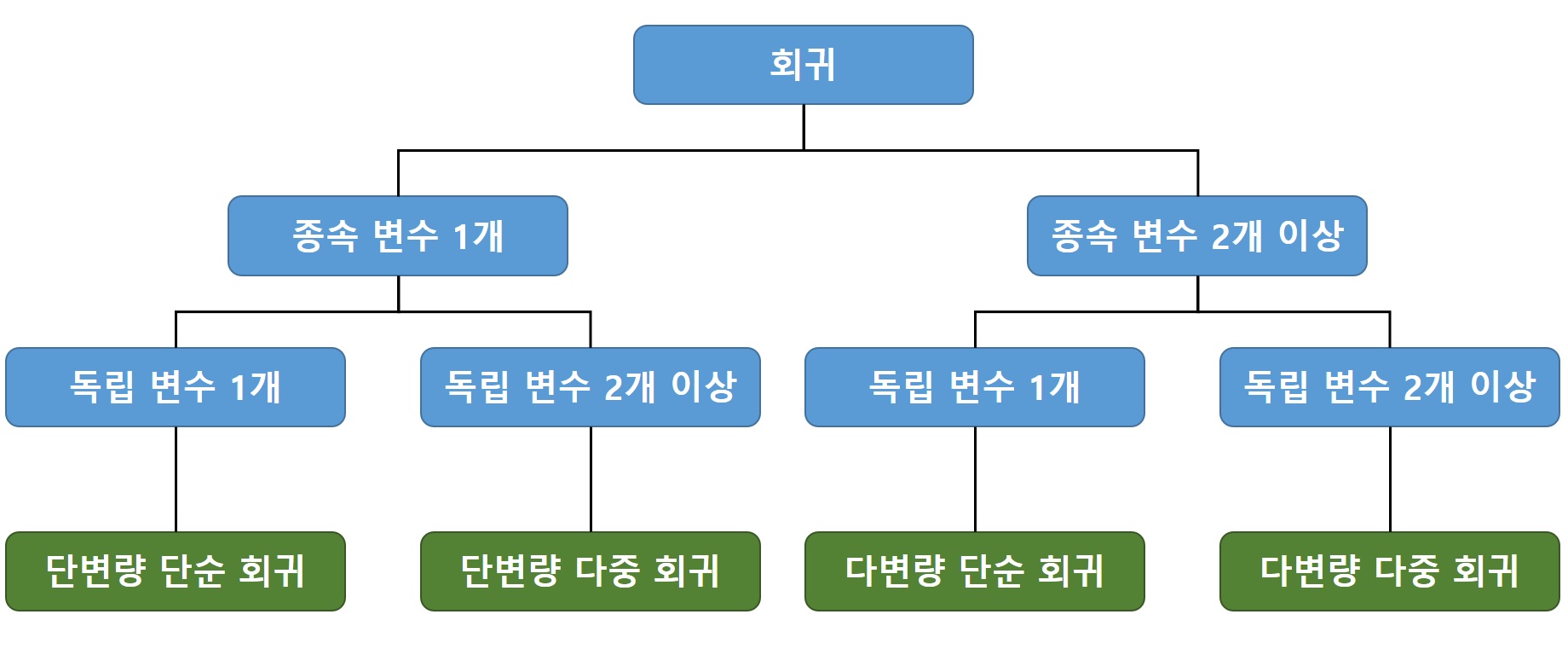
02. 회귀 종류

1) 선형 회귀(Linear Regression)

• 일반적으로 제일 단순한 회귀 방법으로, 독릭 변수와 종속 변수 사이의 관계를 대표하는 직선를 찾는 모델이다.
  

[참고: https://curriculum.cosadama.com/machine-learning/3-2/#google_vignette]

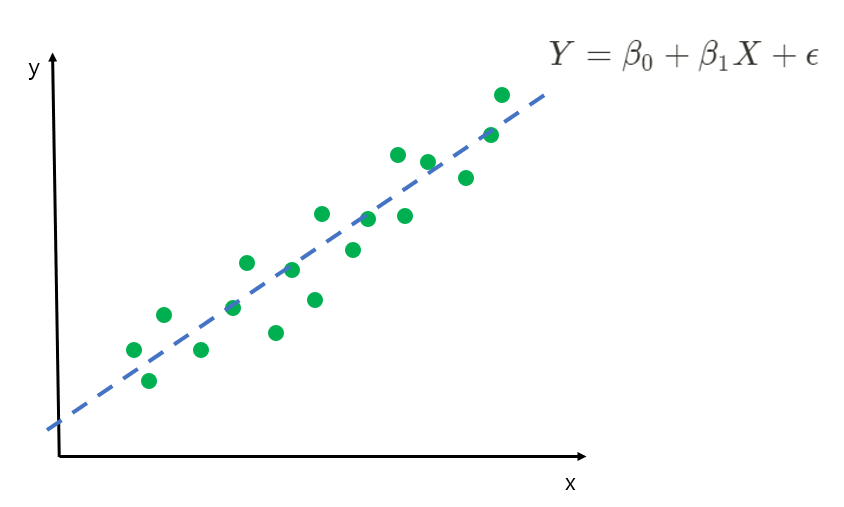
2) 로지스틱 회귀(Logistic Regression)

• 이진 분류와 같이 연속적인 값이 아닌 이산적인 값을 예측하기 위한 모델이다. 이진 분류란 둘 중에 하나를 결정하는 문제이다.
  

• 0과 1사이 값이 없기 떄문에 직선을 표현하기 어렵다. 즉 선형 회귀가 적합하지 않다. 데이터를 정확하게 표현하게 위해서는 S자 형태가 되어야 한다. 이때 대표적으로 사용하는 함수가 시그모이드 함수이다.

[참고: https://velog.io/@stand_hyo/]

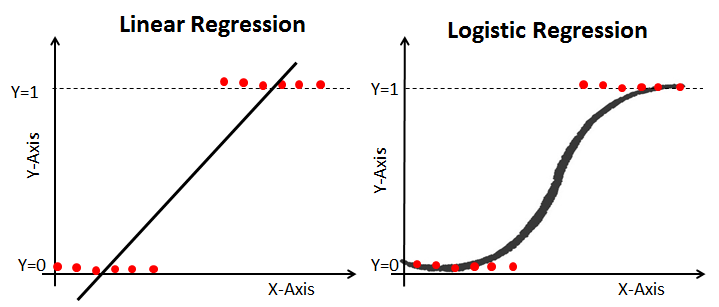
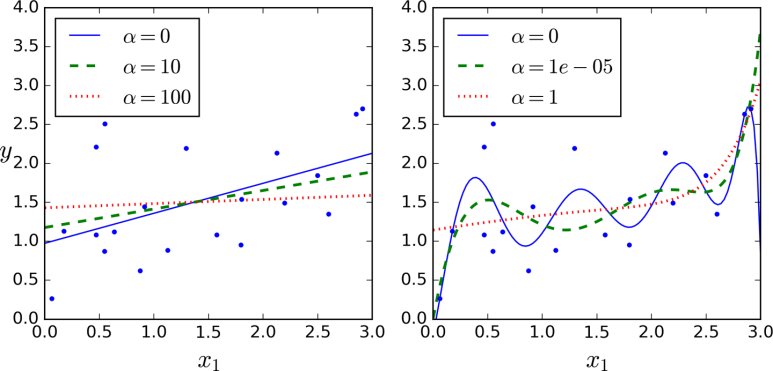
3) 릿지 회귀(Ridge_regression)

• 릿지 회귀는 선형 회귀의 변형된 형태로, 모델의 과적합을 방직하기 위해서 규제(Regularization)을 추가한 회귀이다. 모델의 복잡성을 줄이고 일반화 성능을 향상시키기 위해서 사용하는 모델이다.
  

[참고: https://blog.naver.com/ajskdlf64/221371694376]

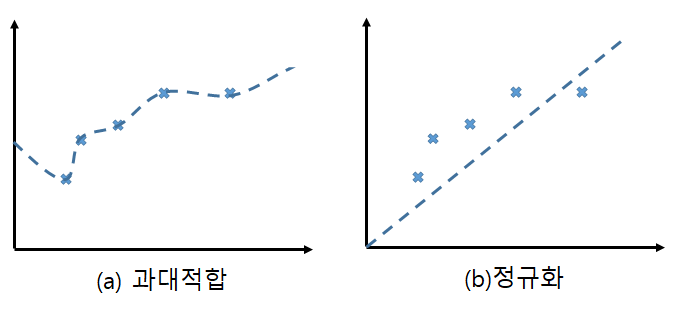
4) 라쏘 회귀(Lasso Regression)

• 라쏘 회귀는 선형 회귀의 변형된 형태로 모델의 과적합을 방지하고 변수 선택을 위해서 정규화를 추가한 모델이다. 라쏘 회귀는 일부 회귀 계수를 정확히 0으로 만들어서 불필요한 변수를 제거한다. 쉽게 설명하면 Dropout 처럼 연결을 끊음으로써 과적합을 방지한다.
  

[참고: https://m.blog.naver.com/pmw9440/221992720025]

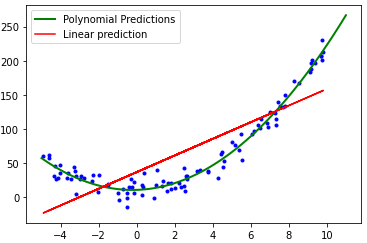
5) 다항 회귀(Polynomial Regression)

• 다항 회귀는 독립변수와 종속변수 사이의 비선형의 관계를 찾기 위한 모델이다. 선형 회귀에서 표현하지 못한 문제를 표현할 수 있다. 독립변수에 대한 다항식을 사용하여 종속 변수와의 관계를 설명한다.
  

[참고: https://velog.io/@ckh0824]

03. 끝마치며

• 이번 포스팅에서는 회귀에 대한 설명과 분성 유형, 변수에 따른 회귀 구분과 회귀의 종류에 대해서 설명하였다. 회귀라는 문제는 통계적으로 활용되었지만 이를 AI의 기초적인 표현방식 및 모델로 활용할 수 있다는 점을 알수 있는 시간이었다고 생각이 든다. 앞으로 이렇게 차근차근 AI 관련된 내용을 포스팅할 예정이다.