[ML] : 03. 손실함수 & 최적화 알고리즘
서론
- 손실 함수는 머신러닝 혹은 딥러닝에서 출력값과 사용자가 원하는 값의 출력 오차를 의미한다. 이 오차가 낮을 수록 좋은 모델이라고 할 수 있다. 이때 이 오차의 최소를 찾기 위한 방법이 최적화 알고리즘 혹은 옵티마이저라고 하며, 손실 함수는 문제 따라서 다른 손실함수를 사용한다.
01. 손실 함수
1) 손실 함수(Loss Function)
- 손실(Loss)는 실제 정답과 예측에 차이(오차)를 말하며, 작으면 작을수록 성능이 좋은 모델이라고 할 수 있다. 이러한 손실(Loss)를 정의하는 함수를 손실 함수라고 한다. 손실 함수는 문제 혹은 모델에 따라서 사용하는 손실 함수가 다르다.
2) MSE(Mean Squared Error) : 평균 제곱 오차
-
실제 값과 예측된 결과의 평균 제곱 오차를 정의한다. 매우 간단한 방법으로 차이가 커질 수록 제곱 연산으로 인하여 값이 차이가 뚜렷하게 나타난다. 제곱으로 인해 음수 또한 양수로 되기 때문에 값이 누적된다.
\[MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2\]- $ n $은 데이터 차수
- $ y_i $는 실제 값
- $ \hat{y}_i $는 예측 값
3) RMSE(Root Mean Squared Error) : 평균 제곱근 오차
-
RMSE는 MSE에 Root를 씌은 형태이다. MSE가 값이 계속 커진다는 단점을 보완하기 위해서 고안한 방법으로 왜곡을 줄여 줄수 있다.
\[RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}\]- $ n $은 데이터 차수
- $ y_i $는 실제 값
- $ \hat{y}_i $는 예측 값
4) Binary Crossentropy : 이진 교차 엔트로피
-
이진 분류 문제에서 활용되는 손실 함수로써 예측 확률과 실제 확률 간의 차이를 측정한다.
\[BCE = -\frac{1}{n} \sum_{i=1}^{n} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right]\]- $ n $은 데이터 차수
- $ y_i $는 실제 값
- $ \hat{y}_i $는 예측 확률
5) Categorical Crossentropy : 카테고리컬 교차 엔트로피
-
다중 클래스 분류 문제를 위한 손실 함수로써 각 클래스에 대한 예측 결과와 실제 결과 사이의 오차를 측정한다.
\[CCE = -\sum_{i=1}^{n} \sum_{c=1}^{C} y_{ic} \log(\hat{y}_{ic}\]- $ n $은 데이터 차수
- $ C $는 클래스의 수
- $ y_{ic} $는 데이터 포인트 $ i $의 실제 클래스에 대한 원-핫 인코딩된 벡터
- $ \hat{y}_{ic} $는 데이터 포인트 $ i $에 대한 예측 클래스 확률
6) Sparse Categorical Crossentropy : 정수 카테고리컬 교차 엔트로피
-
Sparse Categorical Crossentropy는 Categorical Crossentropy의 변형으로, 레이블을 원-핫 인코딩 형식이 아니라 단일 정수 형태로 제공할 때 사용된다. 라벨이 (1,2,3,4) 와 같이 정수 형태일때 사용한다.
\[SCCE = -\sum_{i=1}^{n} \log(\hat{y}_{i, y_i}\]- $ n $은 데이터 포인트 차수
- $ y_i $는 데이터 포인트 $ i $의 실제 클래스 레이블(정수 인덱스)
-
$ \hat{y}_{i, y_i} $는 데이터 포인트 $ i $에 대한 예측 클래스 확률 중 실제 클래스 $ y_i $에 해당하는 확률
- $ y $는 종속 변수
7) Focal Loss
-
페이스북에서 발표한 손실함수로써 Retina Net 모델을 학습 시키는데 사용되며, 객체 탐지 문제에서 클래스 균형을 다루기 위해서 제안되었다. Corss Entropy Loss에 가중치를 부여하여 잘못 분류된 예제에 더 집중한다.
\[\text{FL}(p_t) = -\alpha_t (1 - p_t)^\gamma \log(p_t\]- $ p_t $는 모델의 예측 확률. 구체적으로, $ p_t $는 정답 클래스에 대한 모델의 예측 확률
- $ \alpha_t $는 클래스의 불균형을 조정하는 가중치이다. 이는 클래스별로 다를 수 있으며, 일반적으로 $ \alpha_t $는 스칼라 값
- $ \gamma $는 조정 파라미터로, 샘플의 어려움에 따라 손실의 비율을 조정합니다. $\gamma$의 값이 클수록 쉬운 샘플에 대한 손실 기여가 줄어든다.
02. 최적화 알고리즘(Optimizer)
1) 최적화 알고리즘이란?
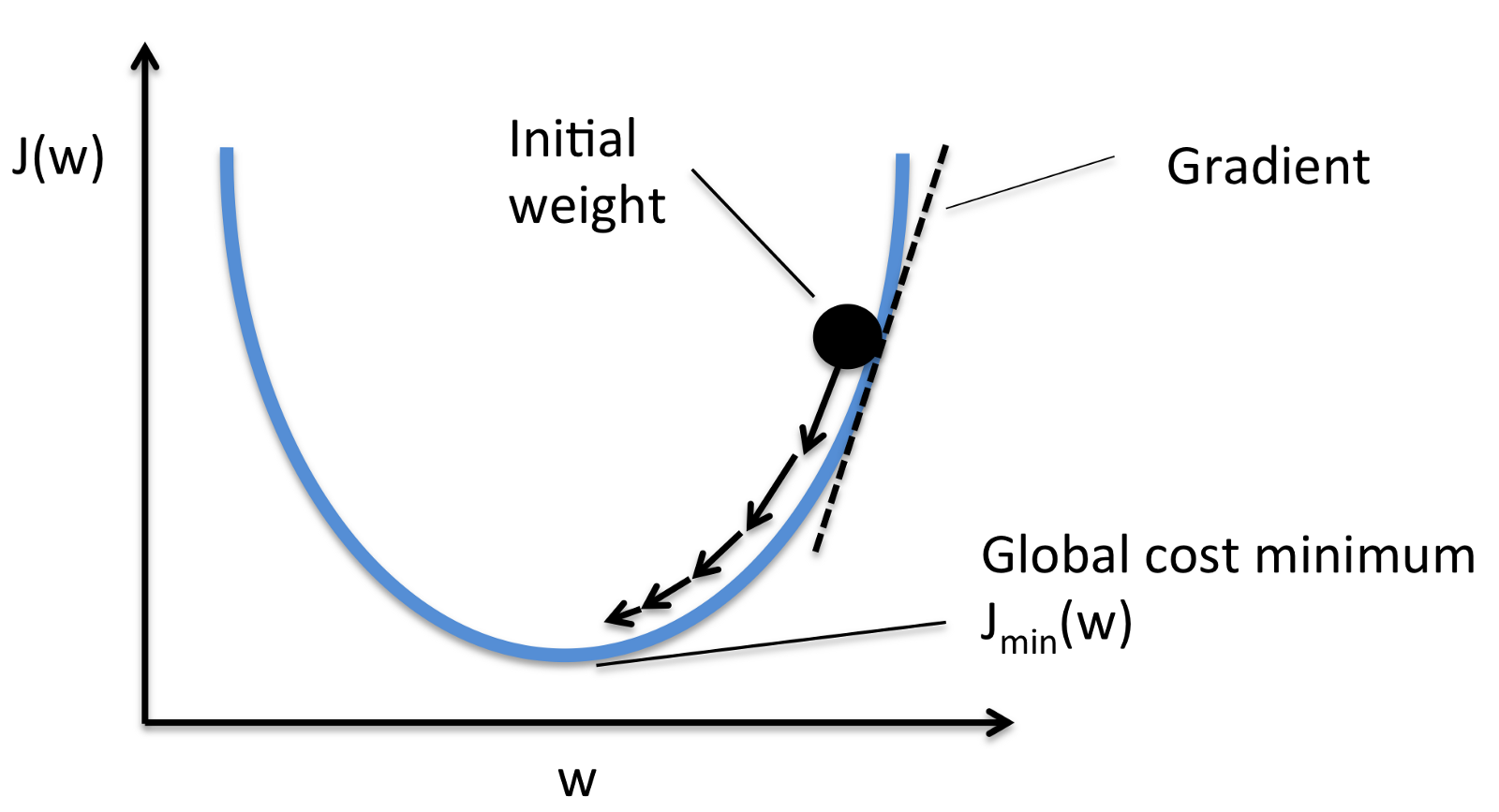
- 최적화 알고리즘은 모델의 손실(Loss)를 최소화 혹은 최대화 하기 위해서 사용되는 방법이다. 학습을 반복함으로써 손실이 적어(보통은 작아지는데 커지는 경우도 있음)지는데, 이때 어떻게 하면 모델이 수렴할 수 있는 최적의 손실값에 빠르게 접근할 수 있게 하는 방법이 최적화 알고리즘이다. 제일 간편한 최적화 알고리즘은 경사 하강법(Gradient DDescent)이다. 아래 사진을 보게 되면 일정 범위로 손실이 적어지는것을 볼 수 있다. 이때 계속 경사를 내려가면서 Loss가 작아지기 떄문에 경사 하강법이라고 한다.
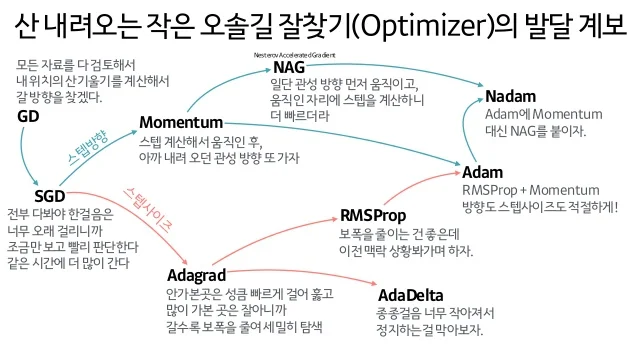
- 최적화 알고리즘은 여러가지 있지만 아래 사진이 대표적으로 잘 정리되어 있어서 가지고 왔다. 이러한 최적화 알고리즘 중 몇가지 설명하고자 한다.
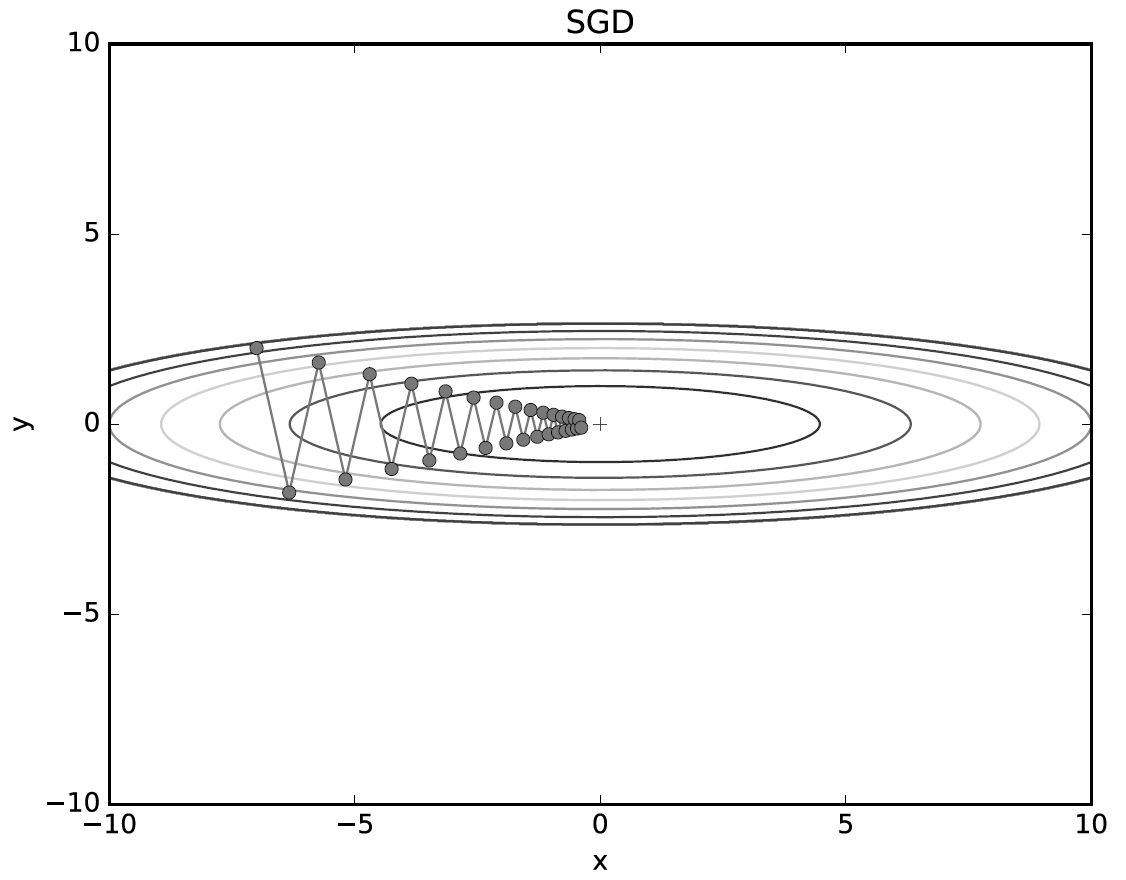
2) 확률적 경사 하강법(SGD : Stochastic Gradient Descent)
- SGD는 경사 하강법의 변형으로 전체 데이터 셋이 아니라 랜덤하게 선택된 소량의 데이터(배치)를 사용하여 파라미터를 업데이트를 한다. 이러한 방식으로 경사 하강법 보다 계산 비용이 크게 절약되고 빠른 업데이트가 가능하다. 또한 한번 학습 하는데 양이 적어 모메로 부족 문제를 해결되고, 학습의 불안정으로 인해 Local Minimun에서 탈불할 수도 있다는 장점이 있다. 하지만 학습이 불안정하여 일정한 성능을 가지지 않는다는 단점을 가진다.
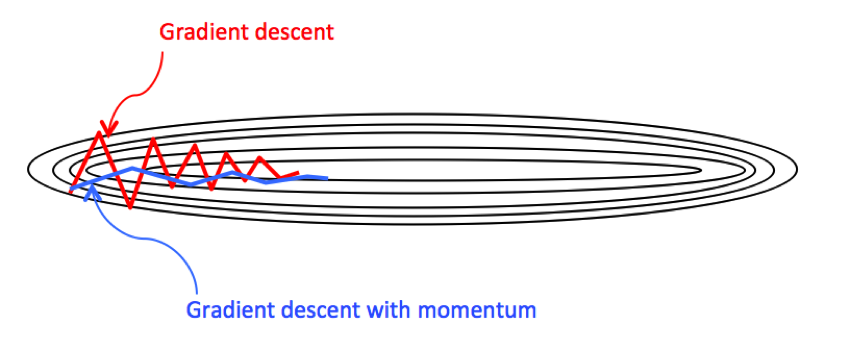
3) 모멘텀(Momentum)
-
경사 하강법을 개선한 최적화 알고리즘으로 현재 학습 단게에서 이전의 학습 방향을 고려한 방법이다. 다시 설명하면 이전 기울기 크기를 고려하여 추가로 이동한다. 이러한 물리적인 관성 개념을 차용한 방법이다. 이러한 방법을 사용하면 Local Minimum에 빠질 가능성이 적어진다.
 [참고: https://meme2515.github.io/neural_network/optimizer/]
[참고: https://meme2515.github.io/neural_network/optimizer/]\(v_t = \gamma v_{t-1} + \eta \nabla_\theta J(\theta\)
- $ v_t $는 현재 속도
- $ \gamma $는 모멘텀 계수로, 이전 속도의 영향을 결정(보통 0.9로 설정)
- $ \eta $는 학습률(learning rate)
- $ \nabla_\theta J(\theta) $는 현재 기울기
4) AdaGrad (Adaptive gradient)
-
Adaptive Gradient 줄임말로 매개 변수 마다 개별적으로 학습률을 조정하는 최적화 알고리즘이다. 기울기를 빈도에 따라서 학습률을 적응적으로 조정한다. 자주 업데이터 되는 매게변수의 학습률을 다운시키고 드물게 업데이트 되는 매개변수 학습률을 업 시킨다.
- 축적된 기울기 제곱합 (Accumulated Gradient Squared Sum)
\(G_t = G_{t-1} + (\nabla_\theta J(\theta))^2\) - $ G_t $는 시간 $ t $에서의 기울기의 제곱합.
-
$ \nabla_\theta J(\theta) $는 현재 기울기.
- 파라미터 업데이트 (Parameter Update)
\(\theta \leftarrow \theta - \frac{\eta}{\sqrt{G_t} + \epsilon} \nabla_\theta J(\theta\) - $ \theta $는 모델 파라미터.
- $ \eta $는 초기 학습률.
- $ \sqrt{G_t} $는 기울기의 제곱합의 제곱근.
- $ \epsilon $은 수치 안정성을 위한 작은 값입니다 (보통 $10^{-8}$).
- 축적된 기울기 제곱합 (Accumulated Gradient Squared Sum)
5) RMSprop (Root Mean Square propagation)
-
AdaGrad의 단점을 보완한 방법으로 이전 Step의 기울기를 단순히 같은 비율로 누적 하지 않고 지수이동평균(Exponential Moving Average)을 사용하여 기울기를 업데이트 한다. 결국에는 AdaGrad와 비슷하지만 최근 기울기는 자주 반영하고 오래된 기울기는 조금만 반영한다.
-
지수 이동 평균 (Exponential Moving Average)
\(E[g^2]_t = \beta E[g^2]_{t-1} + (1 - \beta) (\nabla_\theta J(\theta))^2\) - $ E[g^2]_t $는 시간 $ t $에서의 기울기 제곱의 지수 이동 평균.
- $ \beta $는 지수 이동 평균의 감쇠율(보통 0.9로 설정).
-
$ \nabla_\theta J(\theta) $는 현재 기울기.
-
파라미터 업데이트 (Parameter Update)
\(\theta \leftarrow \theta - \frac{\eta}{\sqrt{E[g^2]_t} + \epsilon} \nabla_\theta J(\theta\) - $ \theta $는 모델 파라미터.
- $ \eta $는 초기 학습률.
- $ \sqrt{E[g^2]_t} $는 기울기 제곱의 지수 이동 평균의 제곱근.
-
6) Adam(Adaptive Moment Estimation)
- Momentum과 RMSprop를 결합한 형태의 최적화 알고리즘으로써, 대중적으로 제일 많이 사용하는 최적화 알고리즘이다. Adam은 기울기의 1차 및 2차 모멘트를 추정하여, 학습률을 적응적으로 조정한다. 이는 기울기의 평균과 분산을 모두 고려하여, 각 파라미터에 대한 학습률을 조정함으로써 다양한 기울기 스케일을 효과적으로 처리할 수 있다.
\(\begin{aligned} & \text{1차 모멘트 추정:} \quad m_t = \beta_1 m_{t-1} + (1 - \beta_1) \nabla_\theta J(\theta) \\ & \text{2차 모멘트 추정:} \quad v_t = \beta_2 v_{t-1} + (1 - \beta_2) (\nabla_\theta J(\theta))^2 \\ & \text{1차 모멘트 바이어스 수정:} \quad \hat{m}_t = \frac{m_t}{1 - \beta_1^t} \\ & \text{2차 모멘트 바이어스 수정:} \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t} \\ & \text{파라미터 업데이트:} \quad \theta \leftarrow \theta - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t \end{aligned}\)
- $ m_t $는 시간 $ t $에서의 1차 모멘트 추정치.
- $ v_t $는 시간 $ t $에서의 2차 모멘트 추정치.
- $ \beta_1 $는 1차 모멘트 추정의 감쇠율(보통 0.9로 설정).
- $ \beta_2 $는 2차 모멘트 추정의 감쇠율(보통 0.999로 설정).
- $ \nabla_\theta J(\theta) $는 현재 기울기.
- $ \theta $는 모델 파라미터.
- $ \eta $는 학습률.
03. 끝마치며
- 이번 포스팅에서는 손실함수와 최적화 알고리즘에 대해서 알아 보았다. 대표적으로 몇개 알아 보았지만, 포스팅에서 얘기한거 이외에도 많은 손실함수와 최적화 알고리즘이 있다.
댓글남기기