[ML] : 04. 의사결정트리(Decision Tree)

01. 의사결정트리

1) 의사 결정 트리(Decision Tree)

• 의사 결정 트리는 분류 및 회귀 분석을 위해 사용되는 지도 학습 알고리즘 중 하나이다. 데이터에서 규칙을 찾아서 분류하는 형태이다. if/else 기반의 규칙 기반의 탐색 방법이다. 논리적인 전개가 스무고개와 유사하다. 이를 시각화 하면 트리 구조가 되어 의사 결정 트리라고 한다. 예를 들면 아래 사진과 같이 보여줄 수 있다. 동물을 분류하는 문제에서 아래와 같은 의사결정 트리를 통해서 분류하는 것이다.
  

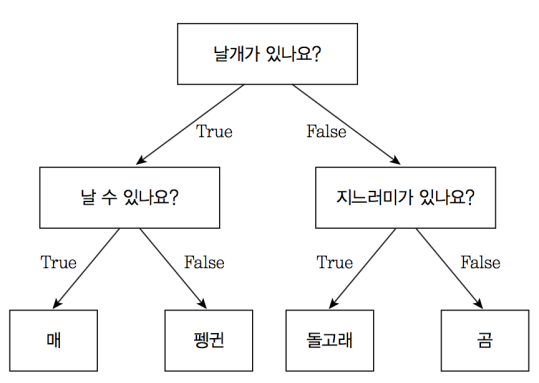
[참고: https://tensorflow.blog]

2) 장점

• 이해와 해석이 가능하여 시각화가 가능하다(하이트 박스 모델)
• 데이터 전처리 필요성이 낮다
• 수치성/범주형 데이터 모두 다루는데 용이하다.
  

3) 단점

• 과적합될 가능성이 높다. 특정 데이터만을 분류하기 위한 규칙이 만들어 질수 있다.
• 데이터의 변화에 민감하여 조금한 변화에도 트리구조가 크게 변형될 수 있다. 이를 해결하기 위해서는 PCA 방법을 활용할 수 있다.
• 트리 생성 과정에서 계산 비용이 많이 들 수 있다.
  

02. 결정트리 생성 과정

• 그림을 통해서 결정트리가 어떤식으로 보여주도록 하겠다. 해당 내용은 여기를 참고하여 만들었다.
  

• 아래 사진처럼 2개의 클래스의 데이터 포인트가 50개 씩 있다면 깊이 따른 결정트리의 생성 과정을 차례대로 보여주겠다. 기초 데이터의 모양은 태극 문양 형태로 서로 겹쳐 있는 형태를 띄고 있다.

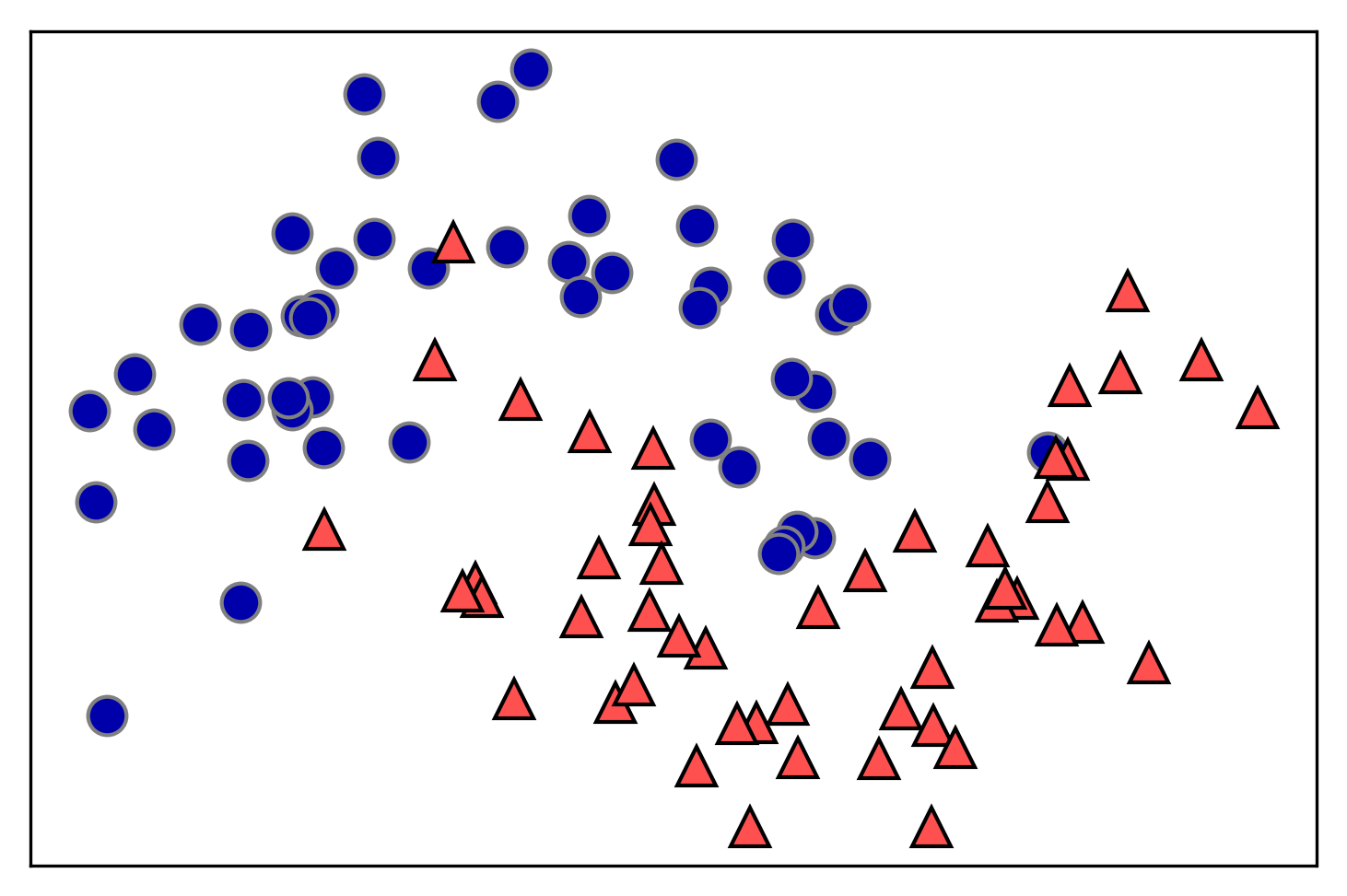
[참고: https://tensorflow.blog]

• 깊이 1를 가지는 의사결정트리의 경우는 아래 사진과 같이 클래스 분류를 제일 잘할 수 있는 선을 그리고 끝이 났다. 하지만 선형적인 분류를 할 수 없는 문제이기 때문에 정확도가 낮아 보인다.

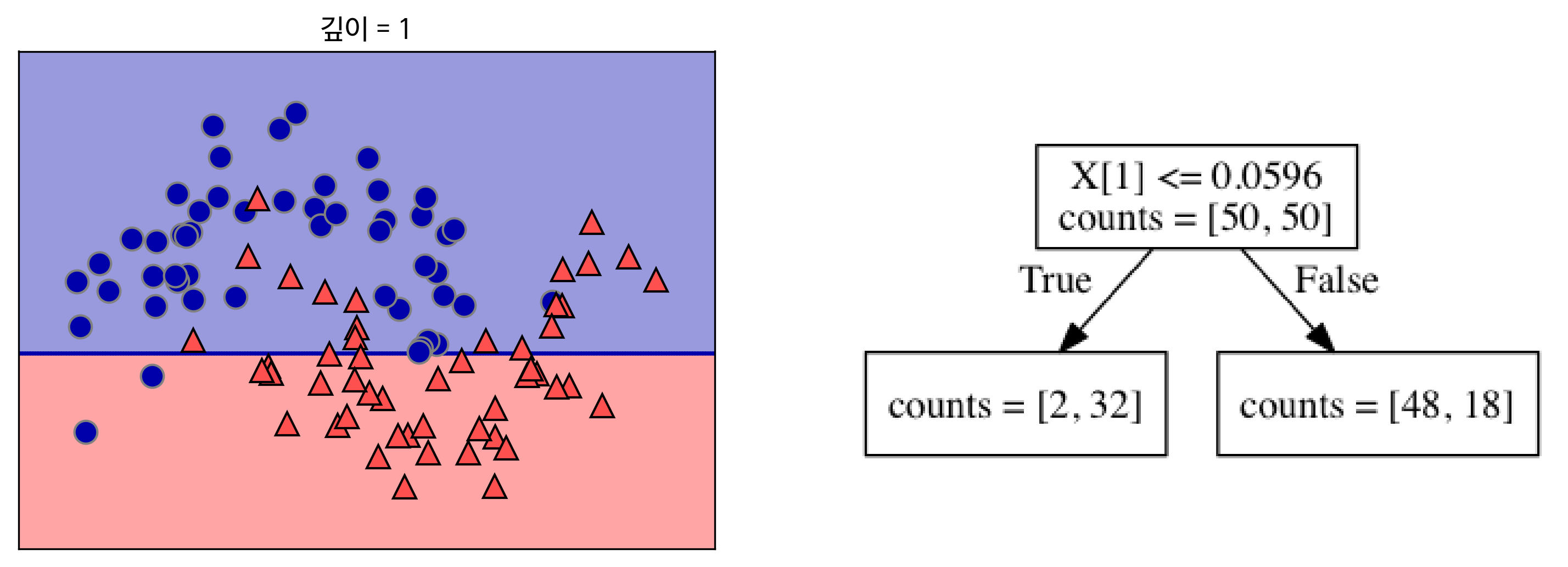
[참고: https://tensorflow.blog]

• 깊이 2의 의사결정트리는 이전 깊이 1의 비해서 더 많은 정확도를 가지는 형태로 분류하였다. 이는 선을 여러개를 그음으로써 이산적인 문제에서 벗어날 수 있었다.
  

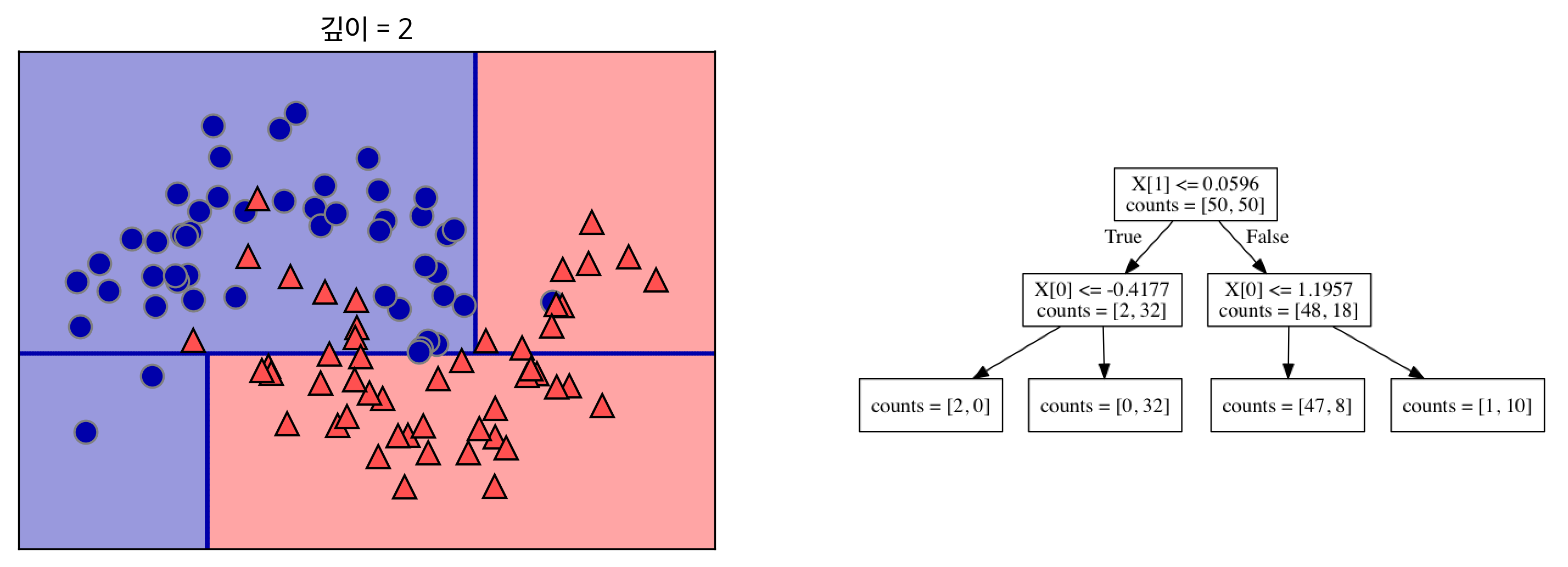
[참고: https://tensorflow.blog]

• 최종적으로 해당 문제를 완벽하게 분류하기 위해서는 깊이 9의 의사결정 트리가 필요하다.
  

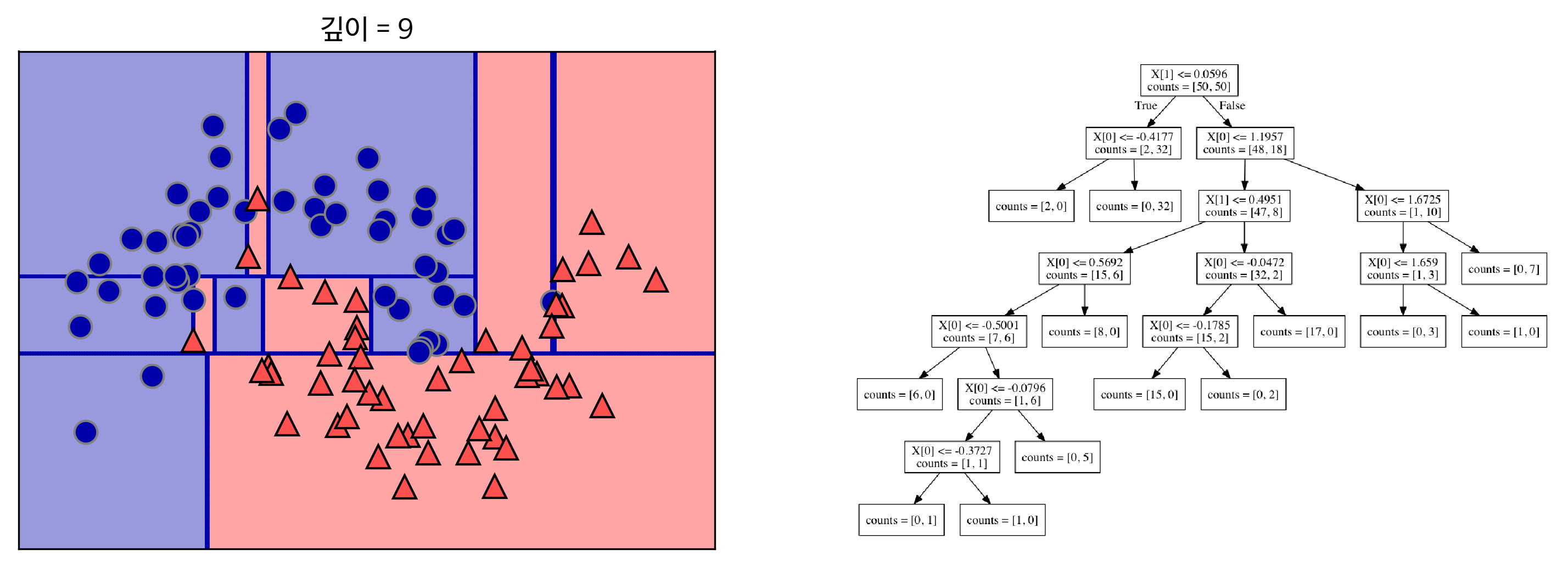
[참고: https://tensorflow.blog]

03. 가지치기

• 가지치기란 의사결정 트리의 과적합을 방지하기 위한 방법이다. 가치지기는 사후 가지치기와 사전 가지치기로 나눌 수 있다.
  

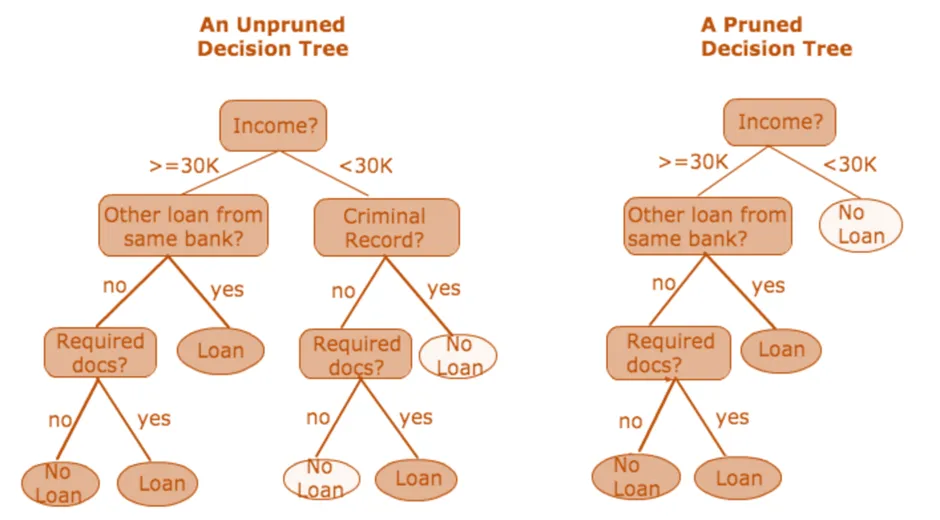
[참고: https://www.geeksforgeeks.org/pruning-decision-trees/]

• 사후 가지 치기(Post-Pruning)
  • 제약 없이 트리를 만든 후 데이터가 적은 노드를 삭제하거나 병합하는 방법.
    
• 사전 가지 치기(Pre-Pruning)
  • 다양한 규제로 트리를 생성을 조기에 중단하는 방법이다. Early Stopping 방법이라고 하여 결정 트리를 조기 중단 하는 방법이다. 트리의 깊이를 제한하거나 최대 말단 노드 수의 제한하는 방법이다.
    

04. 정보량과 지수 불순도

• 의사결정트리에서는 정보량(Information Gain)은 데이터 분할할 때 사용되는 주요한 지표다. 노드 분할 전후로 데이터의 엔트로피를 비교하여 가장 많은 접로ㅑㅇ을 얻응 수 있는 방향으로 분할을 진행한다. 정보량과 함께 지니 불순도 또한 의사결정트리의 분할 기준으로 활용된다.
  

1) 정보량(Information Gain)

• 정보량은 불확실성의 정도를 말한다. 이는 엔트로피로 말할 수 있다. 엔트로피는 데이터의 혼란도를 측정하는 지표로, 값이 낮을 수록 정보량은 높다고 생각하면 된다. 즉 엔트로피가 낮을 수록 해당 분별력이 높기 때문에 정보량이 높다고 할 수 있다.
  

2) 지니 불순도(Gini Impurity)

• 지니 계수(Gini Index)를 이용한 선택 기준이다. 집합의 순도를 측정하며, 순도가 높아지는(지니 불순도가 낮아지는) 방향으로 트리를 확장한다. 계산이 간단하며 연산비용이 적다는 특징이 있다.
  

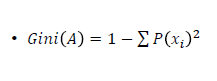
예시 1

• 클래스 1: 90% (0.9)
• 클래스 2: 10% (0.1)

$\text{Gini} = 1 - (0.9^2 + 0.1^2) = 1 - (0.81 + 0.01) = 1 - 0.82 = 0.18 $

• 이 경우, 지니 불순도가 0.18로 낮기 때문에 노드의 데이터가 비교적 순수하다.

예시 2

• 클래스 1: 50% (0.5)
• 클래스 2: 50% (0.5)

$\text{Gini} = 1 - (0.5^2 + 0.5^2) = 1 - (0.25 + 0.25) = 1 - 0.5 = 0.5$

• 이 경우, 지니 불순도가 0.5로 높기 때문에 노드의 데이터가 매우 혼합되어 있다.

05. 끝마치며

• 이번 포스팅에서는 의사결정트리에 대해서 설명하였다. 의사결정트리는 시각화할 수 있어 이해하기 쉽지만 과적합 문제와 범용성 문제로 인해 널리 사용되고 있지는 않다. 하지만 앙상블 학습에서는 약한 분류기로서 사용되는 경우가 있으니 잘알고 있어야 한다.